数量方程式は「フィッシャーの交換方程式」とも呼ばれます。
これは、古典派の貨幣数量説を説明する時に使う式の1つです。
数量方程式
フィッシャーの交換方程式は、「MV=PT」と表されます。
国にあるお金の量(M)×流通速度(V)=物価(P)×取引量(T)

M
Mの意味は「国内にどれくらいたくさんのお金があるか」です。
Mは、国にあるお金の量を表します。

日本銀行が、日本にお金を供給しています。
お金をたくさん供給すると、国にあるお金の量が増えます。
V
Vの意味は「流通速度」です。
「お金がどれくらい繰り返し使われたか」です。
ある期間において、お金が、何回誰かの所得として受け取られたかを表しています。

人々が貯金をしないで、すぐに買い物をする人ばかりなら、お金の流通速度は上がります。
P
Pの意味は「物価」つまり、「モノの値段」です。
「国内の商品の値段の平均」です。

T
Tの意味は「取引数」です。
「販売数」と言ったり、「生産量」と言う人もいますが、同じことです。
企業は、売れる分しか作りません。
つまり「お客さんが買う量=企業が生産する量」です。
古典派の考え方
古典派は、「VとTは、常に一定で変わらないはずだ」と考えています。
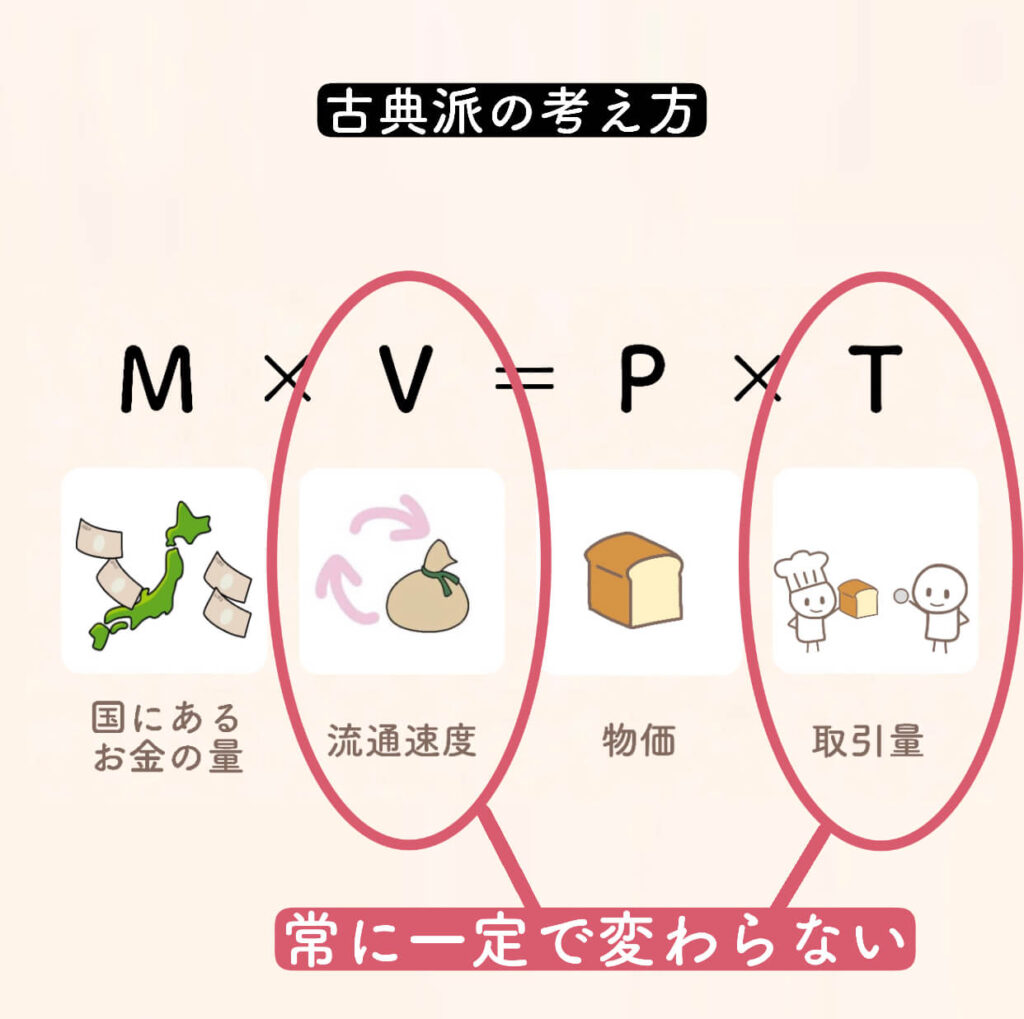
古典派の人は、VとTは、大きな変動がないことを前提としました。
そのため、国にあるお金の量がそのまま物価に影響する、と考えました。
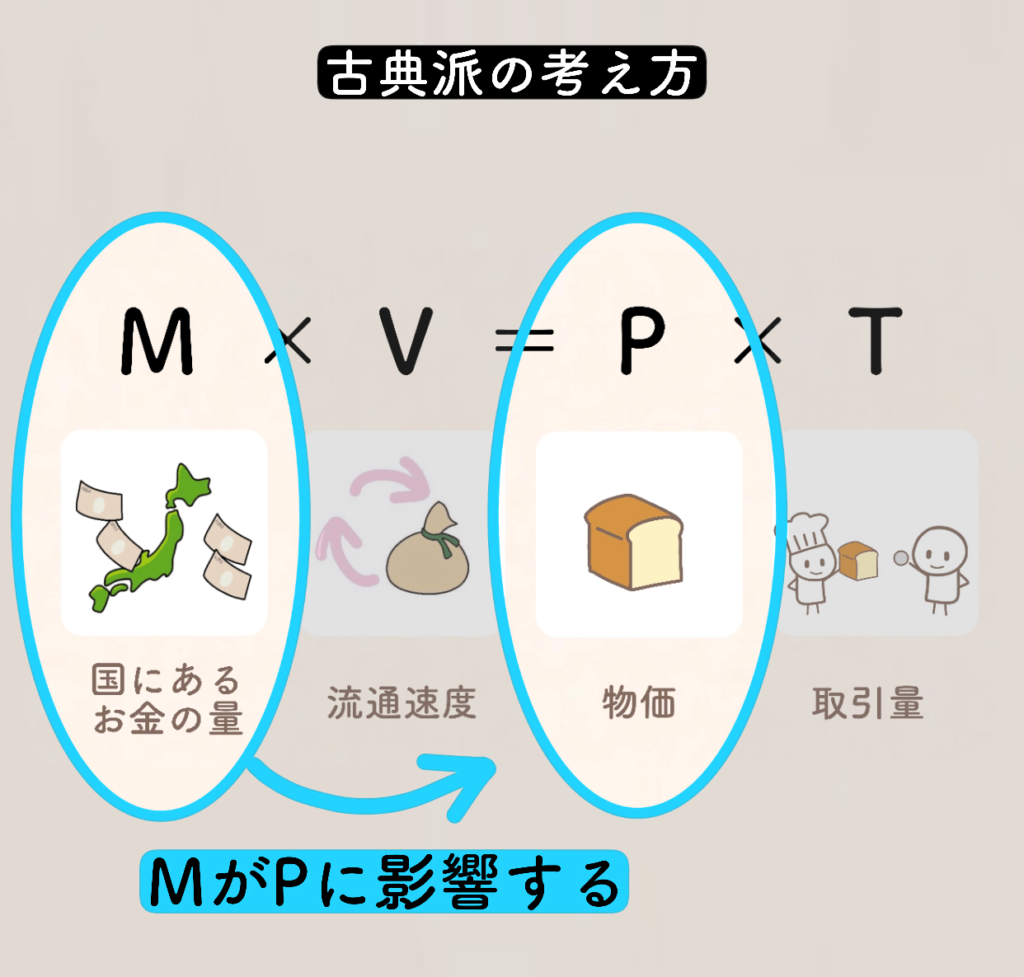
古典派は「MがPに影響する」と考えました。
この考え方が正しければ
国にあるお金の量が増えれば、物価が上がります。
国にあるお金の量が減れば、物価が下がります。
国のお金の量がそのまま物価に影響することを「貨幣数量説」と言います。
貨幣数量説では「物価を上げたいなら、国のお金の量を増やすべき。そして、物価を下げたいなら、国のお金の量を減らすべき」ということを説明します。


